
 咨询热线:400-065-6886
咨询热线:400-065-6886

 咨询热线:400-065-6886
咨询热线:400-065-6886
语法
(1)简单使用情况
统计某中学学生的身高数据如下:
144, 166, 163, 143, 152, 169, 130, 159, 160, 175, 161, 170, 146, 159, 150, 183, 165, 146, 169
(手机上不能完整显示代码或输出,左右滑动屏幕即可)
In [1]:
1 h = c(144, 166, 163, 143, 152, 169, 130, 159, 160, 175, 161, 170, 146, 159, 150, 183, 165, 146, 169)2 boxplot(h)
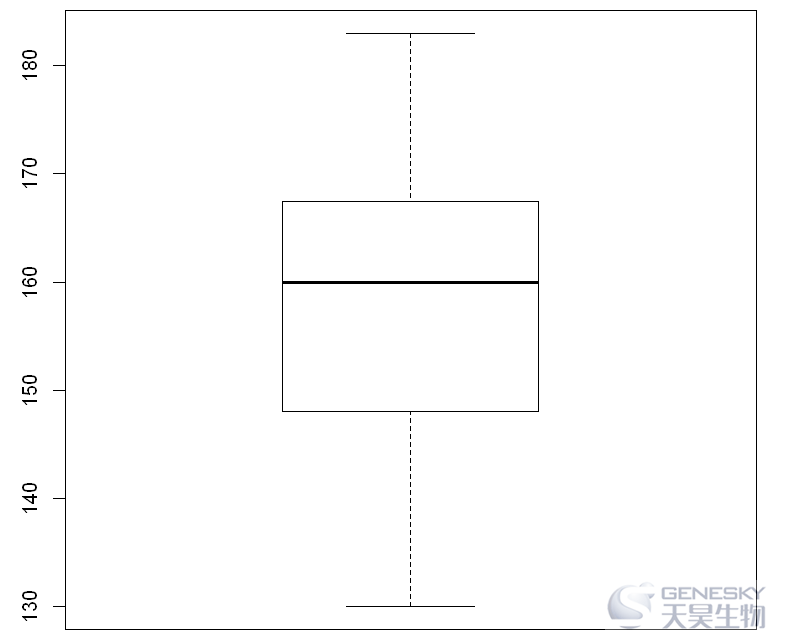
(2)多组的箱线图
某工厂推行新的工作方法,实验组和对照组(原方法)的工作效率(每小时产量),如下面的数据:
试验组:35, 41, 40, 37, 43, 32, 39, 46
对照组:32, 39, 34, 36, 32, 38, 34, 31
绘制其箱线图。
编写R程序如下:
In [2]:
1 x <- c(35, 41, 40, 37, 43, 32, 39, 46, 32, 39, 34, 36, 32, 38, 34, 31)2 f <- factor(rep(c("试验组","对照组"), each=8)) #定义分组因子3 data<- data.frame(x,f) #生成数据框4 data

In [3]:
1 boxplot(x~f,data)
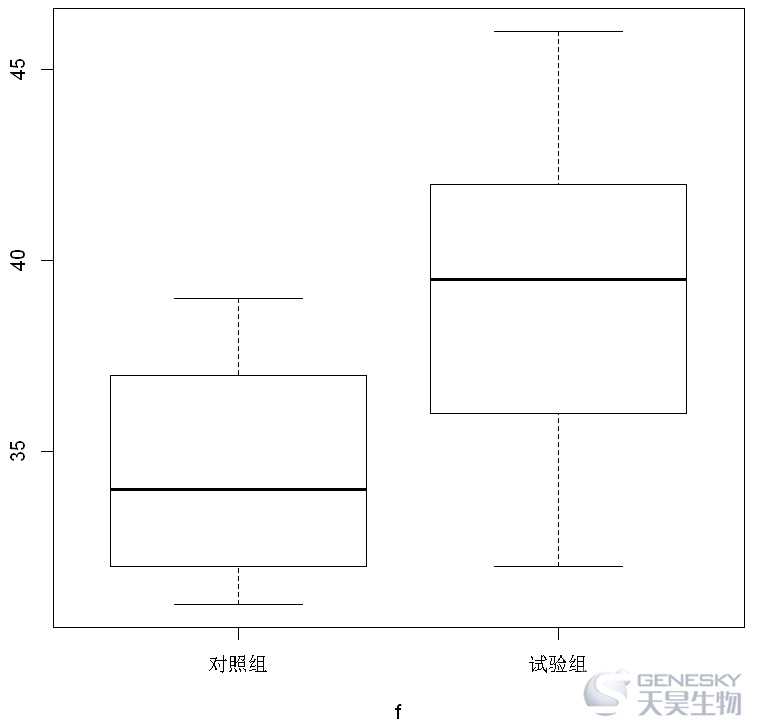
(3)width参数,border参数和col参数的使用
In [4]:
1 x <- c(35, 41, 40, 37, 43, 32, 39, 46, 32, 39, 34, 36, 32, 38, 34, 31)2 f <- factor(rep(c("试验组","对照组"), each=8))3 data<- data.frame(x,f)4 xplot(x~f,data,width=c(1,2), col=c(2,3), border=c("darkgray","purple"))
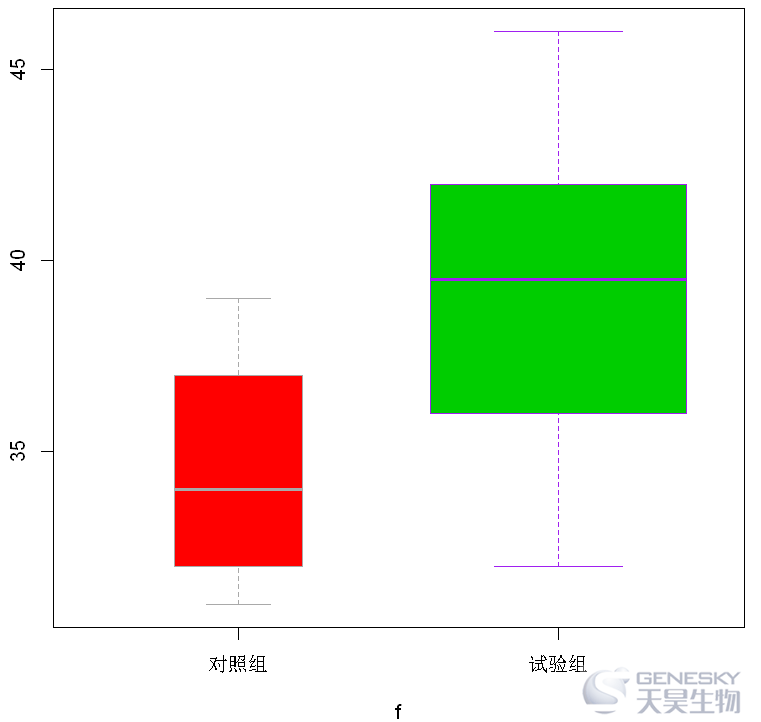
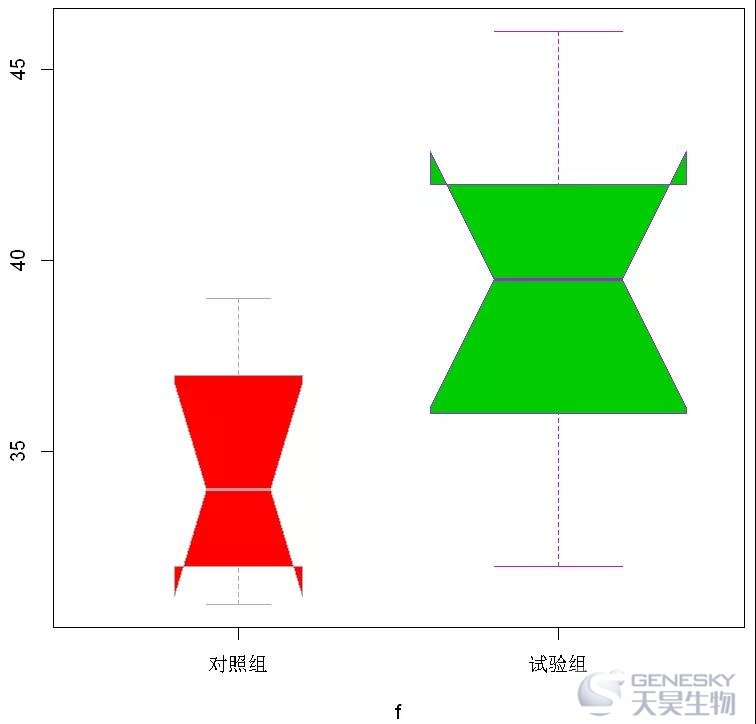
(4)带凹口的箱线图
In [5]:
1 x <- c(35, 41, 40, 37, 43, 32, 39, 46, 32, 39, 34, 36, 32, 38, 34, 31)2 f <- factor(rep(c("试验组","对照组"), each=8))3 data<- data.frame(x, f)4 boxplot(x~f,data,width=c(1,2), col=c(2,3), border=c("darkgray","purple"), notch=TRUE)
读取数据、加载数据
In [6]:
1 df = read.table('alpha.diversity.index.xls',header = T,sep = ' ')2 df
Samples Observed Chao1 ACE Shannon Simpson CoverageA1 151 363.6875 328.2471 0.9143299 0.5851193 0.9980423A2 107 209.2143 209.0519 0.8519641 0.5796722 0.9987263A3 110 201.8333 217.2798 0.7759573 0.5829244 0.9986320B1 119 189.5000 186.3921 1.3215587 0.4164409 0.9988678B2 139 298.7500 285.8452 1.2793320 0.4029692 0.9983017B3 137 275.6667 266.2865 1.2598530 0.4427447 0.9984669C1 142 272.3333 287.8124 1.2834435 0.4747636 0.9983725C2 127 178.0000 233.6027 1.4704978 0.3442275 0.9987971C3 122 267.0909 248.6806 1.4304456 0.3721059 0.9986555D1 67 124.2727 143.6564 0.2969139 0.8897256 0.9991509D2 69 114.7692 153.7493 0.3179932 0.8834281 0.9991745D3 125 195.7143 208.6256 0.6819542 0.7452832 0.9987027
In [7]:
1 attach(df)
In [8]:
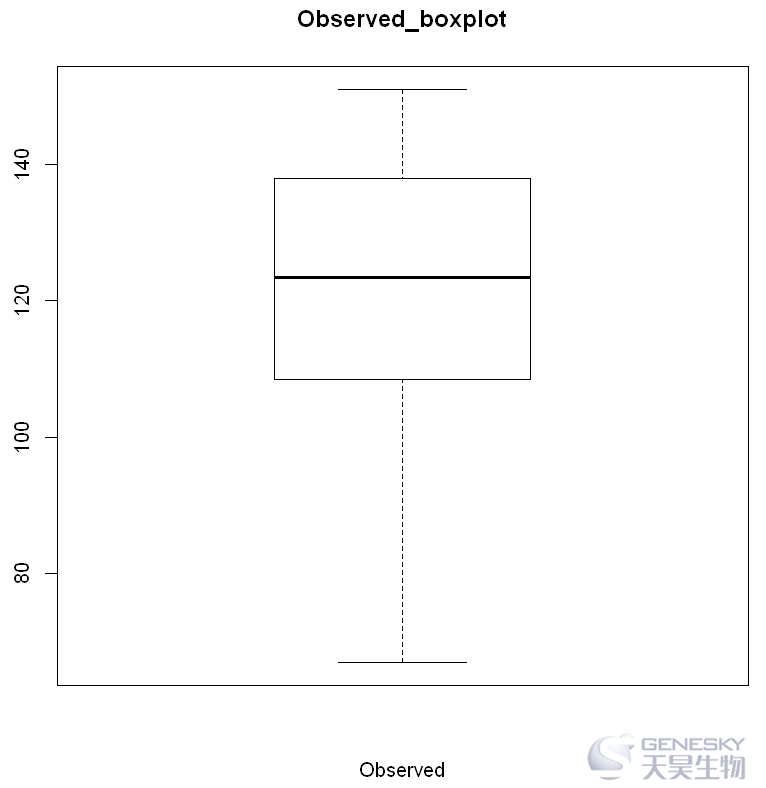
1 boxplot(Observed,xlab = 'Observed',main = "Observed_boxplot")
In [9]:
1 f <- factor(rep(c("A","B","C","D"), each=3))2 data<- data.frame(df, f)3 data
Samples Observed Chao1 ACE Shannon Simpson Coverage fA1 151 363.6875 328.2471 0.9143299 0.5851193 0.9980423 AA2 107 209.2143 209.0519 0.8519641 0.5796722 0.9987263 AA3 110 201.8333 217.2798 0.7759573 0.5829244 0.9986320 AB1 119 189.5000 186.3921 1.3215587 0.4164409 0.9988678 BB2 139 298.7500 285.8452 1.2793320 0.4029692 0.9983017 BB3 137 275.6667 266.2865 1.2598530 0.4427447 0.9984669 BC1 142 272.3333 287.8124 1.2834435 0.4747636 0.9983725 CC2 127 178.0000 233.6027 1.4704978 0.3442275 0.9987971 CC3 122 267.0909 248.6806 1.4304456 0.3721059 0.9986555 CD1 67 124.2727 143.6564 0.2969139 0.8897256 0.9991509 DD2 69 114.7692 153.7493 0.3179932 0.8834281 0.9991745 DD3 125 195.7143 208.6256 0.6819542 0.7452832 0.9987027 D
In [10]:
1 attach(data)
In [11]:
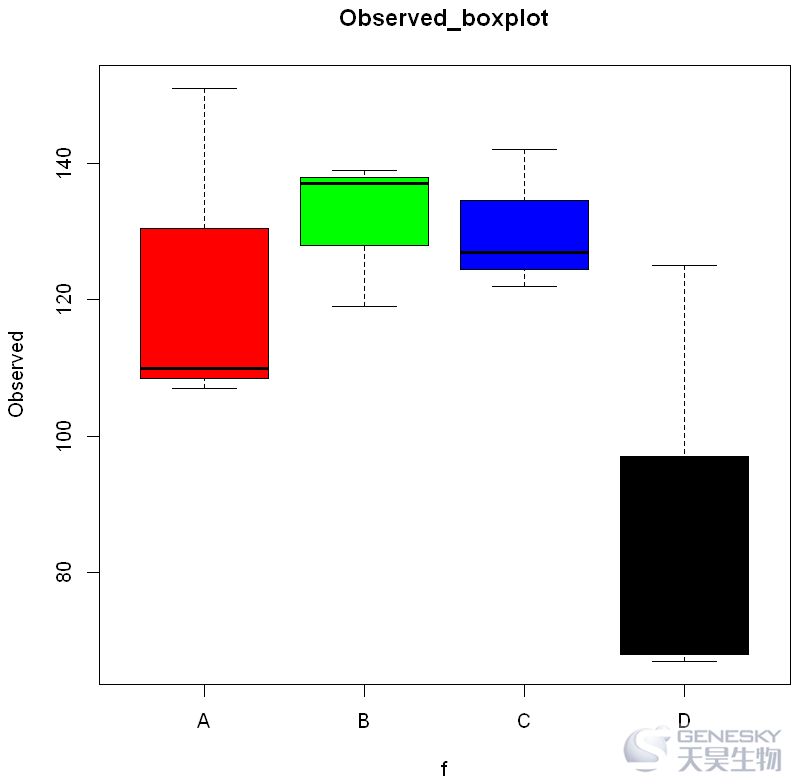
1 boxplot(Observed~f,col=c('red','green','blue','black'),main= "Observed_boxplot",submain='boxplot')
In [12]:
1 par(mfrow = c(2,3))2 boxplot(Observed~f,col=c('red','green','blue','black'),main= "Observed_boxplot",submain='boxplot')3 boxplot(Chao1~f,col=c('red','green','blue','black'),main= "Chao1_boxplot",submain='boxplot')4 boxplot(ACE~f,col=c('red','green','blue','black'),main= "ACE_boxplot",submain='boxplot')5 boxplot(Shannon~f,col=c('red','green','blue','black'),main= "Shannon_boxplot",submain='boxplot')6 boxplot(Simpson~f,col=c('red','green','blue','black'),main= "Simpson_boxplot",submain='boxplot')7 boxplot(Coverage~f,col=c('red','green','blue','black'),main= "Coverage_boxplot",submain='boxplot'

获取更多相关资料,可扫码入群索要哦~
【本群将为大家提供】
分享生信分析方案
提供数据素材及分析软件支持
定期开展生信分析线上讲座

QQ号:1040471849
作者:大熊
审核:有才
来源:天昊生信团

创新基因科技,成就科学梦想