【零基础学绘图】之绘制PCA图（二）-科研进展-上海天昊生物-微生物绝对定量测序、宏基因组测序、甲基化检测、单细胞转录组测序、转录组测序、外泌体检测

【零基础学绘图】之绘制PCA图（二）

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。我们通常使用其中的一维和二维数据进行绘图，用于判断多样性数据分析中样品分类上是否合理。

数据准备

1.数据处理

2.概念介绍

3.PCA分析

plot绘制PCA图

1.不含分组信息的绘图

2.含分组信息的绘图

ggplot2绘制漂亮的PCA图

1.加载ggplot2包，检查输入数据和分组文件，合并数据。

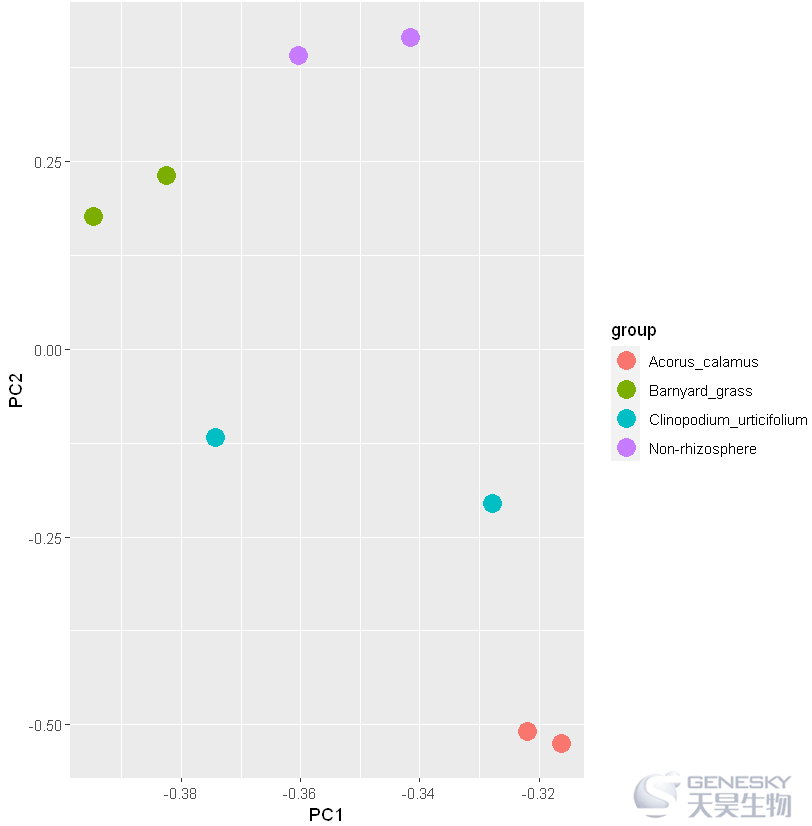
2.绘制分组PCA图

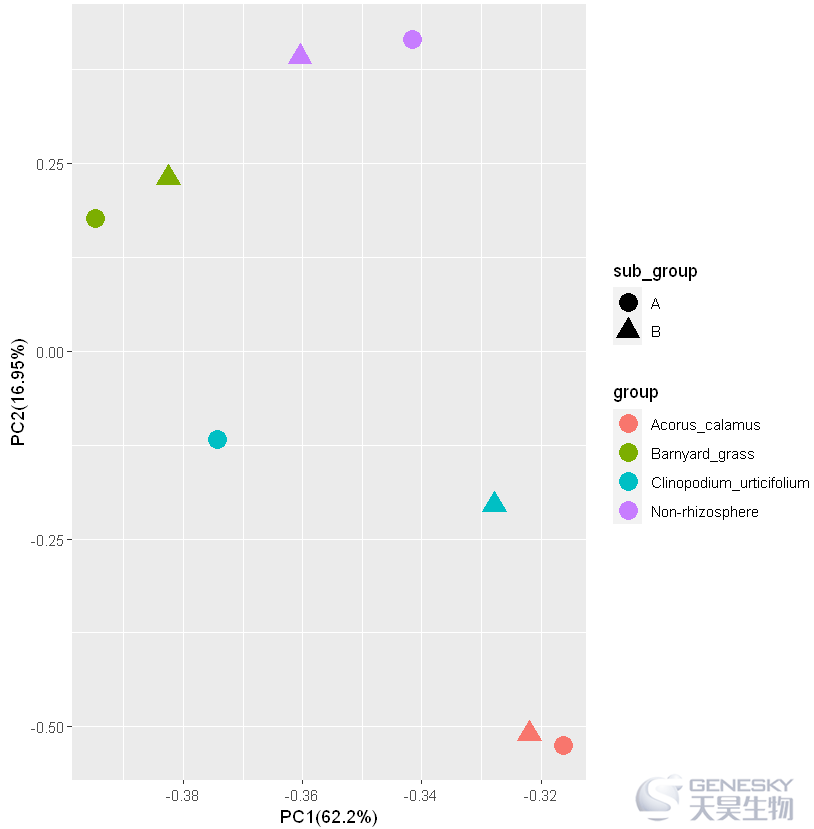
3.绘制带亚组的PCA图

一

数据准备

1. 数据处理
读取文件，并查看文件格式
In [1]:
data = read.table('subsample_otu.tax.0.03.xls',header = T, sep = " ",row.names = 1, check.name = F,comment.char = "", quote= "")
head(data)

Otu[1]:
A1   A2 A3 A4 A5 A6 A7 A8 OTUsize
OTU1   14 6 9 11 15 9 61 97 222
OTU2   28 39 0 1 6 3 0 0 77
OTU3 8 14 11 11 3 7 16 11 81
OTU4 54 61 21 23 4 2 1 0 166O
TU5   6 5 15 7 36 39 1 3 112O
TU6 148  200  11  9  13  10  1  3  395

找到OTUsize所在的列
In [2]:
loc = grep("OTUsize", colnames(data))
loc

Otu[2]:
9

提取OTUsize之前的数据
In [3]:
data = data[,1:loc-1]
head(data)

Otu[3]:
A1 A2 A3 A4 A5 A6 A7 A8
OTU1 14 6 9 11 15 9 61 97
OTU2 28 39 0 1 6 3 0 0
OTU3 8 14 11 11 3 7 16 11
OTU4 54 61 21 23 4 2 1 0
OTU5 6 5 15 7 36 39 1 3
OTU6 148  200  11  9  13  10  1  3

2.概念介绍
R mode ：
是指基于variable的分析，意思就是说在所有的observation里面，来研究variable之间的关系。（observation 大于 variable）
Q mode ：
是指基于observation的分析，意思就是说在所有的variable里面，来研究observation之间的关系。（observation 小于 variable）
princomp ：
基于协方差(covariance) 或者相关矩阵(correlation) 提取的特征(eigen)，也叫     spectral decomposition
只适用于R mode
prcomp ：
基于SVD分解
适用于R mode 和 Q mode

In [4]:
xdim(data)

Otu[4]:
3730 8

8个观测值，3730个变量，观测值的个数大于变量的个数，所以是R mode的数据，princomp和prcomp都可以使用

3.PCA分析

In [5]:

data_pca = prcomp(data,scale=TRUE)

								data_pca

Otu[5]:

Standard deviations (1, .., p=8):

								[1] 2.2307275 1.1645475 0.9231002 0.7127234 0.3329568 0.2961777 0.2398481

								[8] 0.2269067

								

								Rotation (n x k) = (8 x 8):

								          PC1        PC2         PC3         PC4         PC5          PC6

								A1 -0.3163354 -0.5242944  0.32746029 -0.14257138  0.04259692 -0.085790052

								A2 -0.3219150 -0.5091871  0.32997621 -0.15185673 -0.03632209  0.076704375

								A3 -0.3742899 -0.1172604 -0.52020283  0.06934145  0.27364994 -0.692216760

								A4 -0.3277889 -0.2052396 -0.65846139 -0.04926647 -0.25746073  0.581382610

								A5 -0.3947366  0.1769808  0.19555319  0.48456878 -0.08654854  0.136433532

								A6 -0.3825423  0.2305448  0.15936562  0.54747900 -0.05350325 -0.003728952

								A7 -0.3416118  0.4149723  0.09659485 -0.50562126 -0.61714590 -0.255016562

								A8 -0.3604302  0.3915297  0.08206132 -0.39897932  0.68152299  0.293130114

								           PC7         PC8

								A1 -0.50982176 -0.47790989

								A2  0.56274135  0.42576252

								A3  0.01885141  0.12780509

								A4 -0.02190783 -0.09828963

								A5 -0.47789491  0.53415778

								A6  0.44041736 -0.52776502

								A7 -0.01012305 -0.01053616

								A8  0.01073030 -0.01902565

rotation（载荷矩阵）
In [6]:
data_pca$rotatio

Otu[6]:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8
A1	-0.3163354	-0.5242944	0.32746029	-0.14257138	0.04259692	-0.085790052	-0.50982176	-0.47790989
A2	-0.3219150	-0.5091871	0.32997621	-0.15185673	-0.03632209	0.076704375	0.56274135	0.42576252
A3	-0.3742899	-0.1172604	-0.52020283	0.06934145	0.27364994	-0.692216760	0.01885141	0.12780509
A4	-0.3277889	-0.2052396	-0.65846139	-0.04926647	-0.25746073	0.581382610	-0.02190783	-0.09828963
A5	-0.3947366	0.1769808	0.19555319	0.48456878	-0.08654854	0.136433532	-0.47789491	0.53415778
A6	-0.3825423	0.2305448	0.15936562	0.54747900	-0.05350325	-0.003728952	0.44041736	-0.52776502
A7	-0.3416118	0.4149723	0.09659485	-0.50562126	-0.61714590	-0.255016562	-0.01012305	-0.01053616
A8	-0.3604302	0.3915297	0.08206132	-0.39897932	0.68152299	0.293130114	0.01073030	-0.01902565

x（得分矩阵）
In [7]:
head(data_pca$x)

Otu[7]:

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8
OTU1	-5.473904	3.8714451	1.025062	-4.0074032	2.73812465	1.3562936	-0.69617039	-0.232975477
OTU2	-1.628707	-3.1273091	2.262112	-0.5625380	-0.13332691	0.1758814	0.50210427	0.427617906
OTU3	-1.588757	-0.3395338	-0.142335	-0.6403745	-0.06728727	-0.1348358	0.53193412	-0.008971471
OTU4	-4.421300	-6.2513468	1.470565	-1.4061384	-0.02607401	-0.2792422	0.40394234	0.093156537
OTU5	-3.504735	1.0478361	0.646891	3.9647552	-0.20773890	-0.1259525	0.01174219	-0.130746211
OTU6	-11.802261	-17.2396531	10.654976	-3.9452722	-0.04030091	0.1222261	3.01654802	1.283238685

贡献度查看
In [8]:
summary(data_pca)

Otu[8]:
Importance of components:

                         PC1    PC2    PC3    PC4     PC5     PC6     PC7
Standard deviation     2.231 1.1645 0.9231 0.7127 0.33296 0.29618 0.23985
Proportion of Variance 0.622 0.1695 0.1065 0.0635 0.01386 0.01097 0.00719
Cumulative Proportion  0.622 0.7915 0.8981 0.9616 0.97541 0.98637 0.99356
                           PC8
Standard deviation     0.22691
Proportion of Variance 0.00644
Cumulative Proportion  1.00000

PC1贡献度为0.622，PC2贡献度为0.1695

二

plot绘制PCA图

In [9]:
rotation = data_pca$rotation[,1:2]
rotation

Otu[9]:

	PC1	PC2
A1	-0.3163354	-0.5242944
A2	-0.3219150	-0.5091871
A3	-0.3742899	-0.1172604
A4	-0.3277889	-0.2052396
A5	-0.3947366	0.1769808
A6	-0.3825423	0.2305448
A7	-0.3416118	0.4149723
A8	-0.3604302	0.3915297

1.不含分组信息的绘图
In [10]:
plot(rotation)

Otu[10]:

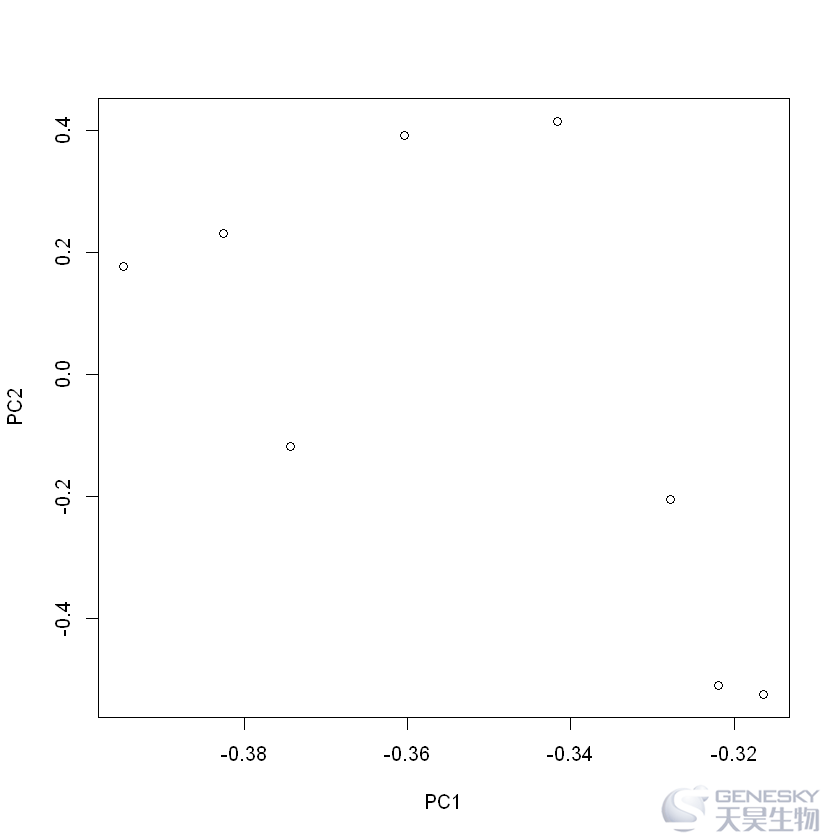
2. 含分组信息的绘图
In [11]:
group = read.table('sample.groups.xls',header = FALSE)
colnames(group)=c('sample','group','sub_group')
group

Otu[11]:

sample	group	sub_group
A1	Acorus_calamus	A
A2	Acorus_calamus	B
A3	Clinopodium_urticifolium	A
A4	Clinopodium_urticifolium	B
A5	Barnyard_grass	A
A6	Barnyard_grass	B
A7	Non-rhizosphere	A
A8	Non-rhizosphere	B

In [12]:
pcolor_group = rainbow(length(unique(group$group))) #利用rainbow函数选择颜色
pcolor_group

Otu[12]:
'#FF0000FF' '#80FF00FF' '#00FFFFFF' '#8000FFFF'

In [13]:
color = color_group[as.numeric(factor(group$group))]color

Otu[13]:
'#FF0000FF' '#FF0000FF' '#00FFFFFF' '#00FFFFFF' '#80FF00FF' '#80FF00FF' '#8000FFFF' '#8000FFFF'

In [14]:
plot(rotation,col = color ,pch = c(21,22,23,24)[group$group])
legend('topright',legend = levels(group$group),col = color_group,pch=c(21,22,23,24))
title('PCA')

Otu[14]:

三

利用ggplot2绘制散点图

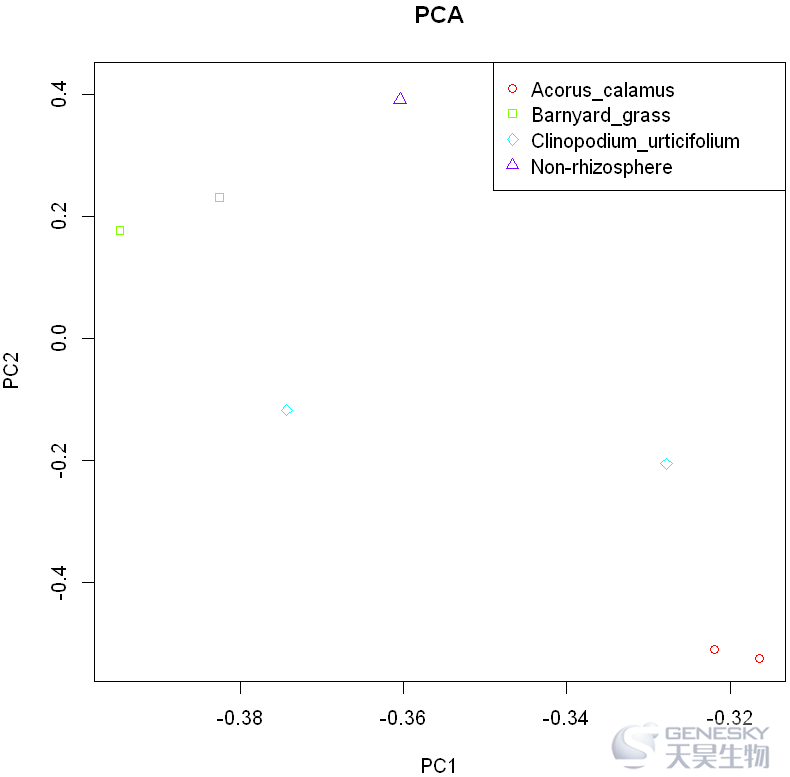
1. 加载ggplot2包，检查输入数据和分组文件，合并数据。
In [15]:
# install.packages('ggplot2') #未安装这个包的话，需要先安装ggplot2
library(ggplot2)
Warning message:
"package 'ggplot2' was built under R version 3.6.3"

In [16]:
rotatio
Otu[16]:

	PC1	PC2
A1	-0.3163354	-0.5242944
A2	-0.3219150	-0.5091871
A3	-0.3742899	-0.1172604
A4	-0.3277889	-0.2052396
A5	-0.3947366	0.1769808
A6	-0.3825423	0.2305448
A7	-0.3416118	0.4149723
A8	-0.3604302	0.3915297

In [17]:
Group =read.table('sample.groups.xls',header = FALSE)
colnames(Group) = c('sample','group','sub_group')
Group

Otu[17]:

sample	group	sub_group
A1	Acorus_calamus	A
A2	Acorus_calamus	B
A3	Clinopodium_urticifolium	A
A4	Clinopodium_urticifolium	B
A5	Barnyard_grass	A
A6	Barnyard_grass	B
A7	Non-rhizosphere	A
A8	Non-rhizosphere	B

In [18]:
pca_result = cbind(rotation,Group)
pca_result = data.frame(pca_result)
pca_result

Otu[18]:

PC1	PC2	sample	group	sub_group
A1	-0.3163354	-0.5242944	A1	Acorus_calamus	A
A2	-0.3219150	-0.5091871	A2	Acorus_calamus	B
A3	-0.3742899	-0.1172604	A3	Clinopodium_urticifolium	A
A4	-0.3277889	-0.2052396	A4	Clinopodium_urticifolium	B
A5	-0.3947366	0.1769808	A5	Barnyard_grass	A
A6	-0.3825423	0.2305448	A6	Barnyard_grass	B
A7	-0.3416118	0.4149723	A7	Non-rhizosphere	A
A8	-0.3604302	0.3915297	A8	Non-rhizosphere

2. 绘制分组PCA图
In [19]:
ggplot(pca_result,aes(x=PC1,y=PC2, color=group)) + geom_point(size=5)

Otu[19]:

3. 绘制带亚组的PCA图
In [20]:
ggplot(pca_result,aes(x=PC1,y=PC2, color=group,shape=sub_group)) + geom_point(size=5)

Otu[20]:

In [21]:
ggplot(pca_result,aes(x=PC1,y=PC2, color=group,shape=sub_group)) + geom_point(size=5) + xlab('PC1(62.2%)') + ylab('PC2(16.95%)')

Otu[21]:

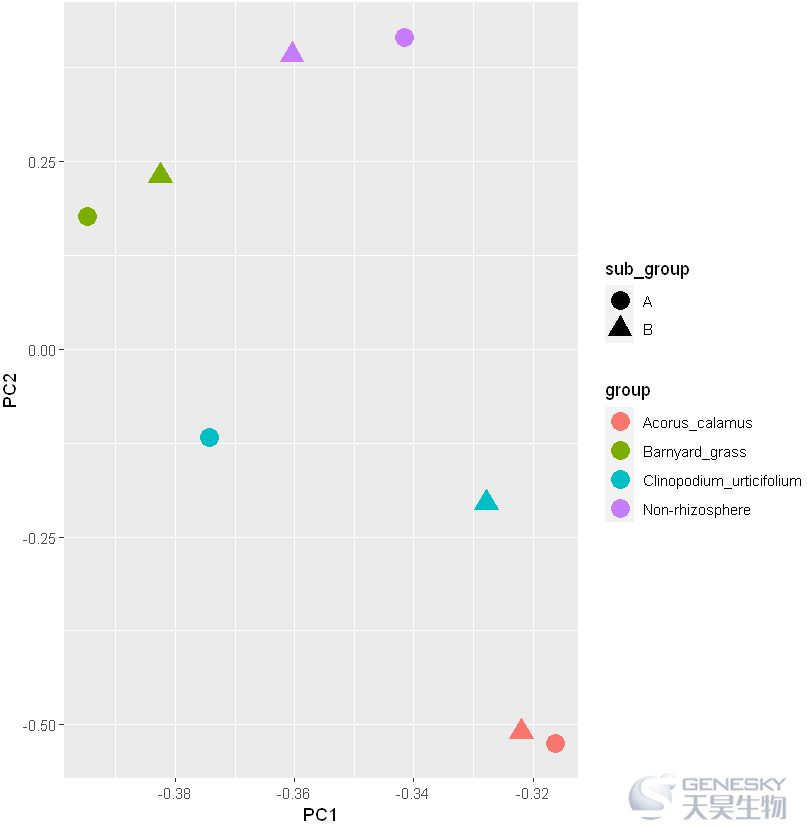
往期链接：

【零基础学绘图】之alpha指数箱体图绘制（一）；

如果您对本文案介绍的方法或代码有疑问，

请扫码添加QQ群沟通

【本群将为大家提供】

分享生信分析方案

提供数据素材及分析软件支持

定期开展生信分析线上讲座

QQ号：1040471849

作者：大熊

审核：有才

来源：天昊生信团

微信扫一扫
关注该公众号